Introduction

Disentanglement or disentangled representation learning in the context of statistical machine learning is the deriving or uncovering of independent generative factors $z_i \in R^c$ given an input observation $x \in R^d$. These generative factors are often called latent variables where $c$ denotes the latent dimension. A generative model that satisfies disentanglement not only learns a low-dimensional representation in $R^c$ that can sufficiently reconstruct the input observation $x$, but also a representation space in which variables are independent from each other. This independence often gives rise to interpretability: given a disentangled model trained on airplane images, for example, the latent space may explicitly encode $z_1 = \text{color}$, $z_2 = \text{width}$, and $z_3 = \text{height}$. An illustrative example of disentanglement is given in the figure below. $ \DeclareMathOperator{\p}{\mathrm{p}} % probability p $ $ \DeclareMathOperator{\q}{\mathrm{q}} % probability q $ $ \DeclareMathOperator{\KL}{\mathrm{KL}} % KL Divergence $ $ \DeclareMathOperator{\d}{\mathrm{d} !} % a small nudge to z $ $ \DeclareMathOperator{\Var}{\mathrm{Var}} % variance $ $ \DeclareMathOperator{\Q}{\mathrm{Q}} % event space Q $ $ \DeclareMathOperator{\EX}{\mathbf{E}} % expected value $

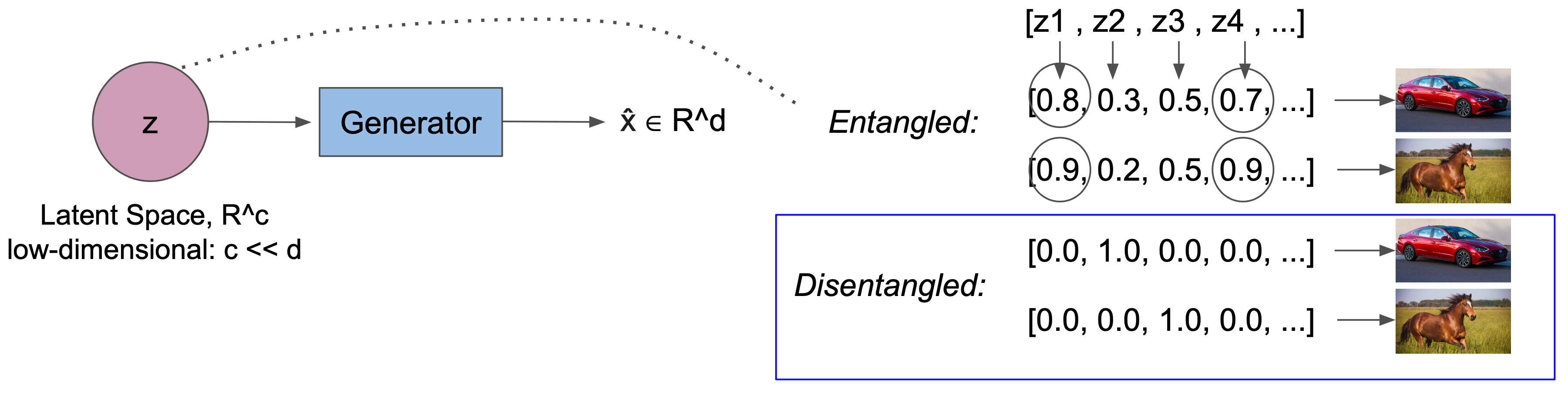
Brief Survey on Disentanglement

Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) are two of the prominent deep learning frameworks for generative modeling. However, their vanilla versions do not naturally give rise to disentanglement. In fact, most machine learning models have features and latent variables that are entangled either due to high correlation in input observations or to specific failure modes. For example, neuron $k$ of layer $j$ in a neural network can get activated by both or either one of sharp corners and bright regions, without necessarily distinguishing between them.

Certain works have mentioned disentanglement as a key component for transferring knowledge across domains and tasks in unsupervised learning, and for inserting compositional properties into neural networks [1]. However, proof for this lacks in the literature, and the independence constraint among the latent variables may not necessarily lead to more realistic outputs. In fact, previous studies showed that this constraint often lead to higher reconstruction errors [2, 3]. Still yet, disentanglement is a promising future direction for explainable and interpretable machine learning models.

Disentanglement Models

Generative models that tackle the problem of disentanglement typically impose constraints in the form of regularization to enforce independence among latent variables. Examples from the literature include shifting the distribution of the variational posterior $q(z|x)$ [2] or variational prior $q(z)$ [4] near prior $p(z)$, using the correlation among the latent variables as an auxiliary loss term [3], and encouraging the covariance matrix $\Sigma_{q(z)}$ of the latent distribution to be as close as possible to the identity matrix $I$ [5]. In the present post, we will be exploring a) InfoGAN [6] and b) $\beta$-VAE [2] which are generative models that tackle the problem of disentanglement. Models and frameworks for disentanglement heavily rely on information theory, and we provide a concise summary of the related concepts in the next section.

Information Theory Background

The self-information of an event $X = x$ is given as

\[I(X = x) = -\log{p(X = x)}\]

This captures the basic intuition that unlikely events have more information compared to likely events. The amount of uncertainty in a probability distribution is given by Shannon entropy:

\[H(X) = E_{x \sim p(x)}[I(x)] = - E_{x \sim p(x)}[\log{p(x)}]\]

Joint entropy of two (discrete) random variables $X$ and $Y$ is denoted as:

\[H(X, Y) = E_{x,y}[-\log{p(x, y)}] = - \sum_{y \sim p_Y(y)} p(x, y) \log{p(x, y)}\]

Conditional entropy of a (discrete) random variable $X$ given another (discrete) random variable $Y$ is the average conditional entropy of $Y$:

\[H(X | Y) = E_{y}[H(x | y)] = - \sum_{y \sim p_Y(y)} p(y) \sum_{x \sim p_X(x)} p(x | y) \log{p(x | y)}\]

We can further transform $H(X|Y)$:

\[\begin{align*} H(X | Y) &= - \sum_{y \sim p_Y(y)} \sum_{x \sim p_X(x)} p(y) p(x | y) \log{p(x | y)} \\ &= - \sum_{y \sim p_Y(y)} \sum_{x \sim p_X(x)} p(x, y) \log{p(x | y)} \\ &= - E_{x, y} [\log{p(x | y)}] \quad \text{by } p(x, y) = p(y) p(x | y) \\ &= - \sum_{y \sim p_Y(y)} \sum_{x \sim p_X(x)} p(x,y) \log{\frac{p(x,y)}{p(y)}} \\ &= - \sum_{y} \sum_{x} p(x,y) \log{p(x,y)} + \sum_{y} \sum_{x} p(x,y) \log{p(y)} \\ &= H(X, Y) - H(Y) \quad \text{by marginalization: } p(y) = \sum_{x} p(x,y) \end{align*}\]

Special cases for the conditional entropy include $H(X|Y) = 0$ if and only if $X$ is completely determined by $Y$, and $H(X|Y) = H(X)$ if and only if $X$ and $Y$ are independent random variables.

Mutual information $I(X;Y)$ is the amount of information that can be obtained about one random variable by observing another random variable. In other words, it is a measure of how correlated two random variables $X$ and $Y$ are such that the more independent the variables are the lesser is their mutual information. Formally,

\[\begin{align*} I(X ; Y) &= \sum_{x,y} p(x,y) \log{\frac{p(x,y)}{p(x)p(y)}} \\ &= \sum_{x,y} p(x,y) \log{p(x,y)} - \sum_{x,y} p(x,y) \log{p(x)} - \sum_{x,y} p(x,y) \log{p(y)} \\ &= - H(X,Y) + H(X) + H(Y) \\ &= H(X) - H(X | Y) \\ &= H(Y) - H(Y | X) \quad \text{by } H(X | Y) = H(X,Y) - H(Y) \end{align*}\]

Kullback–Leibler (KL) Divergence is a measure of dissimilarity between two distributions $\p$ and $\q$. It is said to preserve local information as opposed to global information. Formally,

\[\begin{align*} \text{KL Divergence} = \KL{(\p || \q)} &:= - \sum_{x}^{} \p(x) \log \q(x) + \sum_{x}^{} \p(x) \log \p(x) \\ &= \sum_{x}^{} \p(x) \log \frac{\p(x)}{\q(x)} \\ &= - \sum_{x}^{} \p(x) \log \frac{\q(x)}{\p(x)} \end{align*}\]

KL Divergence has a few important properties:

1. It is a non-negative measure: $\KL{(\p || \q)} \geq 0$
2. It is non-symmetric: $\KL{(\p || \q)} \neq \KL{(\q || \p)}$
3. If $\p$ and $\q$ are identical distributions, we would have $\KL{(\p || \q)} = 0$ and $\KL{(\q || \p)} = 0$.

Information-Theoretic Frameworks of Disentanglement

Now that we have covered disentanglement in the context of statistical machine learning with a brief introduction and survey, and have formalized the relevant information theory background, we can derive information-theoretic frameworks of disentanglement using the aforementioned a) InfoGAN and b) $\beta$-VAE models. In doing so, we’ll be proving key statements and properties of the two models, and motivating the theory behind them.

InfoGAN

InfoGAN’s first distinction from a vanilla GAN is that it samples a random vector that is not only composed of $z$, the latent features for input observation $x$, but also $c$, the latent features for the label $y$ associated with $x$. It should be noted here that this is an unsupervised approach, and the ground truths for $y$ are not provided. To contrast, conditional GANs also incorporate $c$ where it explicitly refers to semantic class labels and is know a priori or given by the dataset, whereas InfoGAN samples $c$ from a prior distribution $p(c)$. InfoGAN tries to learn meaningful feature representations by maximizing the mutual information $I(c; G(z,c))$. This requires evaluation $p(z|x)$ which is intractable and/or difficult to compute, and therefore InfoGAN uses the variational approach just like its counterparts in unsupervised generative modelling.

InfoGAN Formulation

The formal objective function of InfoGAN is:

\[\min_G \max_D V_I(D, G) = V_{\text{GAN}}(D, G) - \lambda I(c; G(z, c))\]

where $G$ and $D$ denotes the generator and the discriminator networks respectively, $I(\cdot)$ denotes the mutual information measure, $V_{\text{GAN}}(D, G)$ is the standard adversarial loss in GANs, and $\lambda I(c; G(z, c))$ is the regularization term where $\lambda$ is the regularization constant which is $<1$ as recommended in the original paper.

In the context of InfoGAN, the standard adversarial loss takes the form:

\[V_{\text{GAN}}(D, G) = E_{x \sim p_{\text{data}}(x)}[\log{D(x)}] + E_{z \sim p_z(z), c \sim p(c)} [\log{(1 - D(G(z, c)))}]\]

We can rewrite the mutual information component as:

\[\max I(c; G(c,z)) = \max H(c) - H(c | G(z, c)) = \min H(c | G(z,c)) \quad \text{since } H(c) \text{ is constant}\]

The intuition is that we would like $H(c|G(z,c))$ to be $0$ ideally, which would in turn mean that $c$ is completely determined by $G(z, c) = \hat{x}$. The fact that the latent variables $c$ which represent attributes can be learnt from the generated data $\hat{x}$ alone resonates with the unsupervised learning theory. It should also be noted that $G(z, c) = \hat{x}$ refers to the output of the generator in InfoGAN which is a function of $z$ and $c$.

Now that we have established the reasoning behind maximizing mutual information $I(c; G(z,c))$, we can formulate the mathematics behind this maximization procedure. It turns out that this term is hard to maximize directly as it requires access to the posterior $p(c|x)$. Therefore, we will have to perform variational mutual information maximization, which obtains a lower bound mutual auxiliary distribution $Q(c|x)$ to be swapped with the true posterior $p(c|x)$. $Q(c|x)$ will be represented with a neural network.

Using the variational mutual information maximization and the change of variable $c = c’$ where $c \sim p(c)$ and $c’ \sim p(c | x)$, we can rewrite the mutual information as:

\[\begin{align*} I(c; G(z, c)) &= H(c) - H(c | G(z, c)) \\ &= H(c) + \int \int p(c = c', X = G(z,c)) dc' dz \\ &= H(c) + E_{x \sim G(c,z), c' \sim p(c | x)}[\log p(c' | x)] \\ &= H(c) + E_{x \sim G(c,z)} E_{c' \sim p(c | x)} [\log{p(c' | x)}] \\ &= H(c) + E_{x \sim G(c,z)} E_{c' \sim p(c | x)} [\log{(\frac{p(c' | x)}{Q(c' | x)} \cdot Q(c' | x)}] \\ &= H(c) + E_{x} E_{c} [\log{(\frac{p(c' | x)}{Q(c' | x)}}] + E_{x} E_{c'} [\log{Q(c' | x)}] \quad \text{by } \log{\frac{AB}{C}} = \log{\frac{A}{C} + \log{B}} \\ &= H(c) + E_{x}[D_{\text{KL}}(p || Q)] + E_{x} E_{c'}[\log{Q(c'|x)}] \end{align*}\]

where $D_{\text{KL}}(p||Q)$ is the KL-divergence between the two distributions $p$ and $Q$. Therefore, omitting the expectation of the KL-divergence term, we can write:

\[I(c; G(z, c) = \hat{x}) \geq H(c) + E_{x} E_{c'} [\log{Q(c' | x)}]\]

where the right-hand side is known as the lower bound on mutual information which we can optimize. One remaining issue is that sampling from $p(c|x)$ is another difficult task; thus we need to replace it by a known distribution from which we can sample $c$ with ease. For this, we refer to the following lemma from the original paper which holds for two random variables $X$ and $Y$, and a function of them $f(x,y)$ under suitable regularity conditions:

\[E_{x \sim p(x), y \sim p(y|x)} [f(x,y)] = E_{x \sim p(x), y \sim p(y|x), x' \sim p(x,y)} \,[f(x', y)]\]

This helps us rewrite the final form of the lower bound as:

\[\begin{align*} I(c; G(z, c) = \hat{x}) &\geq H(c) + E_{c \sim p_C(c)} E_{x} E_{c'} [\log{Q(c' | x)}] \\ &\geq H(c) + E_{c \sim p_C(c)} E_{x} [\log{Q(c' | x)}] = \mathcal{L}_I(c, G(z,c)) \end{align*}\]

Finally, we can replace the mutual information with the lower bound, $I(c;G(z,c)) = \mathcal{L}_I(c, G(z,c))$, and arrive at the final objective function for InfoGAN:

\[\min_G \max_D V_I(D, G) = V_{\text{GAN}}(D, G) - \lambda \mathcal{L}_I(c, G(z, c))\]

This final form of the objective function only requires sampling from $p(c)$ which is a known distribution, and therefore is suitable for tractable optimization.

$\beta$-VAE

$\beta$-VAE is a special variant of the variational autoencoders (VAE) family. The only major distinction $\beta$-VAE has over a vanilla VAE is the addition of a $\beta$ scaling parameter on the KL Divergence term in the objective function:

\[\min\big({|x - \hat{x}|^2 + \beta \KL{(\q(z | x) || \mathcal{N})}}\big)\]

The original paper shows comprehensive experiments which proves that $\beta > 1$ achieves disentanglement by balancing latent channel capacity and independence constraints with reconstruction accuracy.

VAE Formulation

Here we will motivate the problem VAEs tackle, which applies directly to $\beta$-VAE as well. Given a observable set of data $\{x_1, x_2, \ldots, x_n\}$, we want to infer latent (i.e. hidden, non-observable) variables $\{z_1, z_2, …, z_m\}$:

\[\p(z | x) = \frac{\p(z, x)}{\p(x)} = \frac{\p(x | z) \p(z)}{\int{\p(x | z) \p(z) \d z}}\]

The integral decomposition for the probability density $\p(x)$ is difficult to compute in many cases due to the integral being intractable. Variational inference proposes to approximate $\p(z|x)$ by another tractable distribution $\q(z)$ (e.g. family of Gaussian, exponential, etc.), and tries to make $\q(z)$ as similar to $\p(z|x)$ as possible. We can express this objective mathematically by forming it as a minimization problem on KL Divergence. Let’s first rewrite KL Divergence in an easier form:

\[\begin{align*} \KL{(\q(z) || \p(z | x))} &= - \sum_{z} \q(z) \log \frac{\p(z | x)}{\q(z)} \\ &= - \sum_{z} \q(z) \log \frac{\frac{\p(x, z)}{\p(z)}}{\q(z)} \\ &= - \sum_{z} \q(z) \log{\bigg(\frac{\p(x, z)}{\q(z)} \frac{1}{\p(x)} \bigg)} \\ &= - \sum_{z} \q(z) \bigg(\log{\frac{\p(x, z)}{\q(z)}} + \log{\frac{1}{\p(x)}} \bigg) \\ &= - \sum_{z} \q(z) \bigg(\log{\frac{\p(x, z)}{\q(z)}} - \log{\p(x)} \bigg) \\ &= - \sum_{z} \q(z) \log{\frac{\p(x, z)}{\q(z)}} + \sum_{z} \q(z) \log{\p(x)} \\ &= - \sum_{z} \q(z) \log{\frac{\p(x, z)}{\q(z)}} + \log{\p(x)} \sum_{z} \q(z) \\ &= - \sum_{z} \q(z) \log{\frac{\p(x, z)}{\q(z)}} + \log{\p(x)} \end{align*}\]

Then, we can rewrite the second term on its own:

\[\log{\p(x)} = \KL{(\q(z) || \p(z | x))} + \underbrace{\sum_{z} \q(z) \log{\frac{\p(x, z)}{\q(z)}}}_{\mathcal{L}}\]

We know that $\log \p(x)$ is constant for a given $x$. Therefore, in order to minimize the KL divergence, we can instead maximize $\mathcal{L}$, which is called the variational lower bound (also known as evidence lower bound or ELBO). This is essentially the objective of variational inference.

Since $\KL \geq 0$, we deduce $\mathcal{L} \leq \log \p(x)$. This is why it is called the lower bound. If one is maximizing the lower bound of a function, then one ends up maximizing the function. We can transform $\mathcal{L}$ into more familiar terms:

\[\begin{align*} \mathcal{L} &= \sum_{z} \q(z) \log{\frac{\p(x, z)}{\q(z)}} \\ &= \sum_{z} \q(z) \log{\frac{\p(x | z)\p(z)}{\q(z)}} \\ &= \sum_{z} \q(z) \bigg(\log \p(x | z) + \log \frac{\p(z)}{\q(z)} \bigg) \\ &= \underbrace{\sum_{z} \q(z) \log \p(x | z)}_{\EX_{\q(z) \sim \Q}{[\log \p (x | z)]}} + \underbrace{\sum_{z} \q(z) \log \frac{\p(z)}{\q(z)}}_{-\KL{(\q(z) || \p (z))}} \end{align*}\]

Now instead of minimizing $\KL{(\q(z)||\p(z|x))}$, we can maximize

\[\mathcal{L} := \EX_{\q(z) \sim \Q}{[\log \p (x | z)]} - \KL{(\q(z) || \p (z))}\]

which could be broken down into two sub-objectives: i) given latent variables $z$, maximize the likelihood of generating observations $x$, and ii) make $q$ as similar as possible to $p$.

We can now assume that $q$ and $p$ are both neural networks corresponding to the encoder and the decoder respectively. Interpreting the neural network as a deterministic function between $x$ (observed data) and $\hat{x}$ (reconstructed data), and assuming that $z \sim$ Multivariate Gaussian Distribution, we end up with:

\[\p(z | x) \p(x | \hat{x}) = e^{-|x - \hat{x}|^2} \implies \EX_{\q(z) \sim \Q}{[\log \p (x | \hat{x})]} = - |x - \hat{x}|^2\]

Then, the loss function (i.e. objective function to minimize) for the VAE becomes:

\[\min\big({|x - \hat{x}|^2 + \KL{(\q(z | x) || \mathcal{N})}}\big)\]

The VAE neural network doesn’t generate $z$ directly since $z \text{~} \mathcal{N}(\mu, \Sigma)$, it generates the parameters of the distribution, namely mean and covariance vectors: $ \mu = [\mu_1, \ldots, \mu_d] \in \mathbb{R}^d$, and $\Sigma = [\sigma_1^2, \ldots, \sigma_d^2] \in \mathbb{R}^d$. Note that we are assuming that the covariance matrix is a diagonal matrix such that the covariance of feature $i$ and $j$ is $0$ if $i \neq j$.

Once we have the mean and variance vectors, we can sample from the distribution defined by the parameters. We can then use this as a generative model, forget about the encoder and simply feed sampled $z$ to the decoder.

References

[1] Irina Higgins, David Amos, David Pfau, Sebastien Racaniere, Loic Matthey, Danilo Rezende, Alexander Lerchner: Towards a Definition of Disentangled Representations. (arxiv - 2018)
[2] Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, Alexander Lerchner: beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. ICLR (2017)
[3] Hyunjik Kim, Andriy Mnih: Disentangling by Factorising (arxiv - 2018)
[4] Alireza Makhzani, Jonathon Shlens, Navdeep Jaitly, Ian Goodfellow, Brendan Frey: Adversarial Autoencoders (arxiv - 2015)
[5] Abhishek Kumar, Prasanna Sattigeri, Avinash Balakrishnan: Variational Inference of Disentangled Latent Concepts from Unlabeled Observations (arxiv - 2017)
[6] Xi Chen, Yan Duan, Rein Houthooft, John Schulman, Ilya Sutskever, Pieter Abbeel: InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. (arxiv - 2016)
[7] Ali Ghodsi’s Lecture on Variational Autoencoder